Game of the day

We played this game during exam supervision sessions to pass the time:

Game name: Slap

Equipment: 52 card deck

No. of players: 2 to 5

---

Instructions

1. Shuffle the deck and deal the cards evenly. (It's okay to have one card extra if say 3 players are playing.)
2. Organise into a pile, but do not look at the cards.
3. Each player takes turns to flip their card and put in the centre. As you flip the cards, you have to shout out a number - the first person shouts 1 or A, second shouts 2, third shouts 3, then 4, 5, 6, 7, 8, 9, 10, J, Q, K, back to A etc.
4. If the shouted number is the same as the flipped card, then you have to slap the card. The first person to slap the card gets all the cards in the centre pile. E.g. when shouted number is 4, flipped card is 4, you slap the pile
5. If you get all the cards, you win. (Note: that way, those who has no cards can still play.)

---

Variations to step 4

1. Silence: do not shout, but keep track of the numbers in your head
2. Plus one minus one: e.g. if shouted number is 4, slap when flipped card is 3 or 5
3. Reverse: start with K, then Q, J, 10, .... 1
4. Challenge: Square for 1, 2 and 3 (so 1 corresponds to 1, 2 to 4, 3 to 9), plus one for 4 to 10, and minus one for J to K.

Can you think of any interesting and thought-provoking ones to add to the list?

Answers to statistics problem

Answers:

(a) r = 0.9903; there is very strong evidence, especially when there are so many data points, to suggest that time increases the number of visitors... tick tock tick tock

(b) v = 28.2 + 31.6d; a = 28.2 (28) is the number of visitors in day 0 (that's probably true, because I didn't install the counter yet), b = 31.6 (32) is the number of visitors increase each day

(c) 11500 visitors

(d) extrapolation is usually inappropriate in statistics as you are working outside the range of the data you are given; in this case, it's 1 ≤ d ≤ 15, and for (c) you are using d = 365, so well outside the range; there is no evidence that the regression line model would hold. But, of course, I'd be very happy to have 11500 visitors in a year!

---

Bonus:

(a) r = 0.9684; there is strong evidence to suggest that time increases the number of different countries

(b) c = 14 + 2.5d; a = 14 is the number of countries in day 0; b = 2.5 (2 to 3) is the number of countries increase each day.

(c) 927 countries

(d) again, extrapolation is usually inappropriate and meaningless; also, there are only 271 different countries in the world, according to the World Factbook! Well, unless I dominate the world...

Playing with colours: Part 1

Statistics problem

This is my path to world domination... muahahahaha.


Kidding... not kidding.

Anyways, here's the raw data:


Now, here are the questions:

(a) obtain the product moment correlation coefficient to 4 significant figures, between the number of visitors and time in days; comment on this coefficient

(b) let day = d and no. of visitors = v; find the equation of the regression line of d on v in the form d = a + bv, where a and b are constants to 3 significant figures; give a practical interpretation of both constants

(c) using the regression line, extrapolate to work out the number of visitors, to 3 significant figures, my blog will have in a year (assuming 1 year = 365 days)

(d) give logical reasons why the method and result in (c) are inappropriate

---

Tips: Should not be difficult if you know the method, but there is a lot of data here - easy to make careless mistakes - so be patient.

Bonus: If you are extremely enthusiastic, do (a) to (d) for the number of countries, c

---

Good luck to all who are doing Statistics 1!

---

Go back to the main post of this week: Hong Kong case studies

What is a rainbow?

Definition 1

---

Definition 2


An optical phenomenon that appears as an arc of the colours of the visible spectrum across the sky when falling water droplets are illuminated by sunlight from behind the observer. The colours are produced by refraction and internal reflection of the sunlight by the water drops.

Two bows may be visible, the inner ring being know as the primary bow and the outer, in which the colours are reversed, as the secondary bow (two internal refractions in the raindrop occur).

---

Go to About Rainbows for more information.

Go back to the main post of this week: Hong Kong case studies

Hong Kong case studies: Part 1

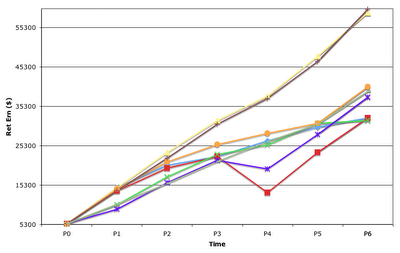
The following case studies are a glimpse of I've done in geography fieldtrips. Here's also a chance to know a bit more about Hong Kong.

1. Chung Hom Kok Beach

Location: South of Hong Kong Island, Hong Kong


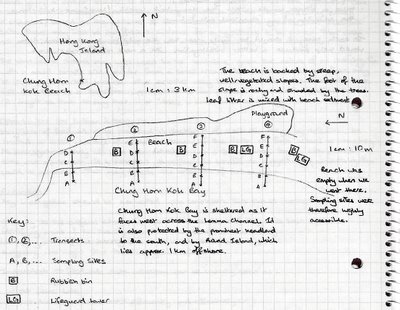
This is a small 150 m, public beach in a rich (suburban) district. When we went there, it was deserted (probably because it was a weekday), and the weather was really bad. But it was peaceful.

We went there to investigate whether longshore drift occurs on this beach. I don't want to bore you with the details, but in essence, our conclusion was that there was no conclusion...

I didn't take any photos here. However, I can summarise Chung Hom Kok as a tiny beach with many bands of beautiful shells.


The picture below is taken from the government website, and they probably filled the beach to make it seem less empty (and come on! the sky wasn't that blue?!):

---

2. Central - Central Business District

Location: Midlevels in Central, North-west Hong Kong Island, Hong Kong


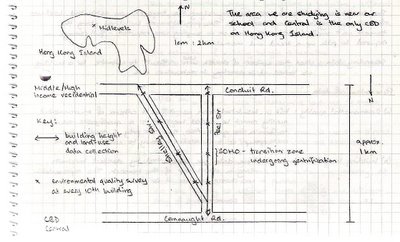
EDIT: The above diagram is slightly inaccurate. Thankfully, I checked with someone before I went into the exam room. It should show the same starting point and different stopping points.

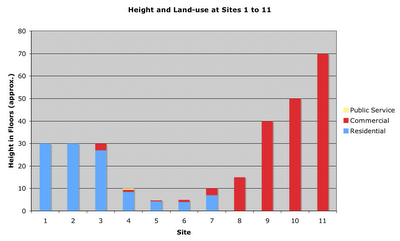
We did an urban transect across Central, one of many CBD's (CBD = Central Business District) in Hong Kong. There, we examined land-use, building height, and environmental quality.

We concluded that Central is similar to the CBD represented by the Burgess model in that there are distinct land-use zones; but what's so unique about Hong Kong is that the residential buildings are very tall, due to the limit of space; hence the buildings start off very tall, then short in the old inner city (known as SoHo), then tall again.


Photos I took are from the inner city (or transition zone) onwards; there's not much to see in the residential areas, unless you want to see my home...

Enjoy (from SoHo to Central):














As you can see, the SoHo area is undergoing a lot of gentrification (the renewal of decaying inner cities). Foreign companies such as starbucks and wildfire, are invading these areas. Nevertheless, there are still signs of Hong Kong culture left, such as the old tram, old advertisement signs, and ancient buildings that will only be maintained.

I did not bother to label each photo, so feel free to ask about them.

---

Read Part 2 here.

Good luck to those who are doing AS Geography!

Sure win?

We're the one in brown:


We'll see...

---

EDIT: Yes! Although, we didn't come first, we became second, which is enough to advance to the second last round.

Go back to the main post of this week: Eclipses